BGSMath Summer Colloquium 2018
BGSMath Summer Colloquium 2018
Dates
10 July 2018
Speakers
Diego Córdoba (ICMAT)
Anna Cima (UAB/BGSMath)
Location
Sala Prat de la Riba (IEC)
Singularities in water waves and drops
Abstract
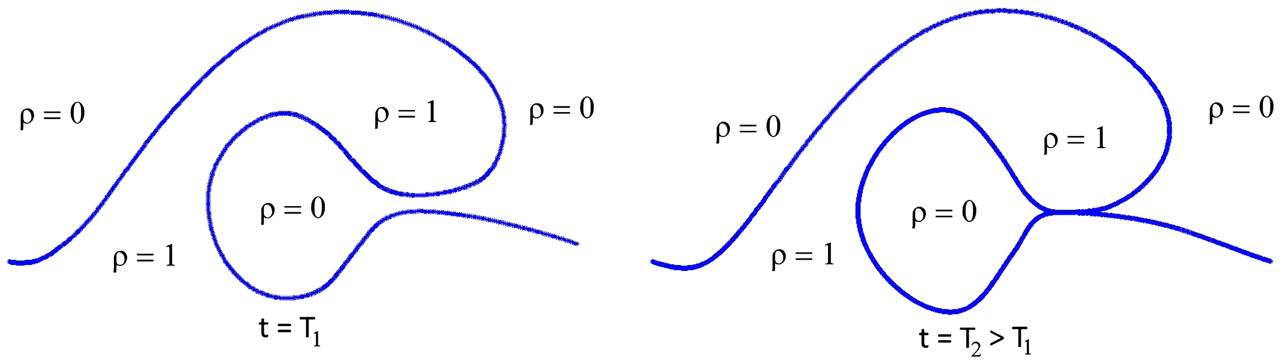
The search for singularities in incompressible fluids has become a major challenge in the area of nonlinear and nonlocal partial differential equations. In particular, the existence, or absence, of finite-time singularities with finite energy remains an open problem for the 3D incompressible Euler equations in the absence of boundaries or in the periodic setting.
A key ingredient in the success of proving the formation of singularities is to identify a scenario in which there is a clear mechanism developing fast vorticity growth, and accurate numerics plays a crucial role in this search.
In this talk, I will discuss on recent progress in the study of the dynamics of the incompressible free boundary Euler equations: water waves and drops. In particular I will focus in two plausible singular scenarios discovered first by numerical simulations which led later to a rigorous proof.
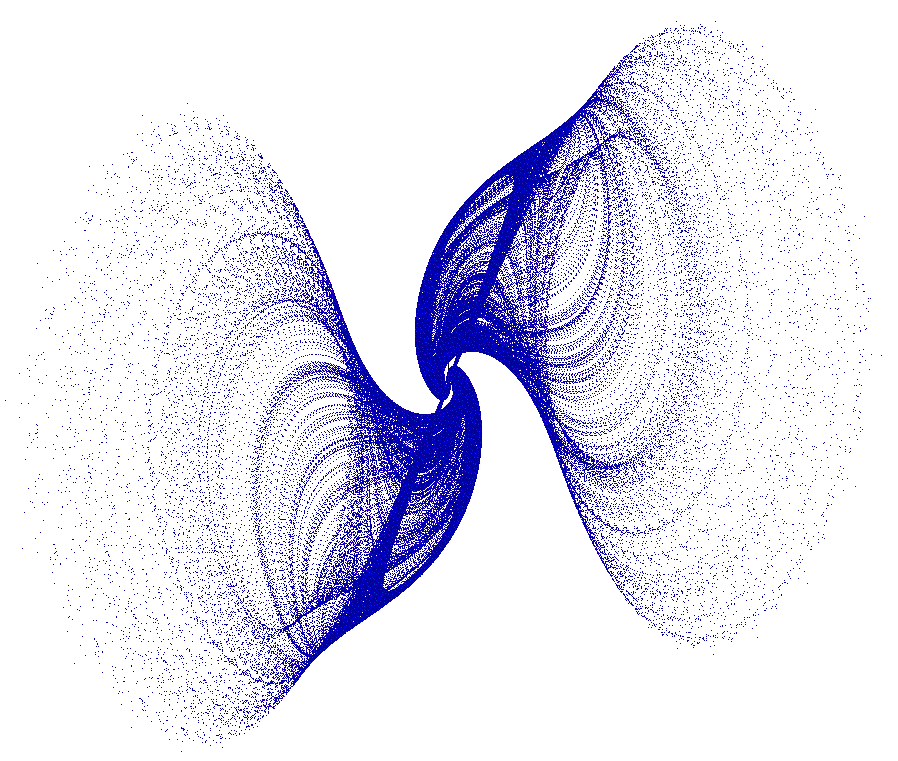
Global Attractors
Abstract
In 1960, Markus and Yamabe proposed a dynamical conjecture. In this talk I’m going to explain the history of its solution and its relationship with the classical Jacobian Conjecture in the polynomial case.
After, I’ll present some results on the discrete version of this conjecture, studying also other conditions on global attractors stablished by La Salle in his book “The Stability of Dynamical Systems”. We give affirmative results as well as some counterexamples.
The talk is based in several papers made in colaboration with Armengol Gasull and Francesc Mañosas..

Dates
10 July 2018
Speakers
Diego Córdoba (ICMAT)
Anna Cima (UAB/BGSMath)
Location
Sala Prat de la Riba (IEC)



Singularities in water waves and drops
Abstract
The search for singularities in incompressible fluids has become a major challenge in the area of nonlinear and nonlocal partial differential equations. In particular, the existence, or absence, of finite-time singularities with finite energy remains an open problem for the 3D incompressible Euler equations in the absence of boundaries or in the periodic setting.
A key ingredient in the success of proving the formation of singularities is to identify a scenario in which there is a clear mechanism developing fast vorticity growth, and accurate numerics plays a crucial role in this search.
In this talk, I will discuss on recent progress in the study of the dynamics of the incompressible free boundary Euler equations: water waves and drops. In particular I will focus in two plausible singular scenarios discovered first by numerical simulations which led later to a rigorous proof.
Global Attractors
Abstract
In 1960, Markus and Yamabe proposed a dynamical conjecture. In this talk I’m going to explain the history of its solution and its relationship with the classical Jacobian Conjecture in the polynomial case.
After, I’ll present some results on the discrete version of this conjecture, studying also other conditions on global attractors stablished by La Salle in his book “The Stability of Dynamical Systems”. We give affirmative results as well as some counterexamples.
The talk is based in several papers made in colaboration with Armengol Gasull and Francesc Mañosas..
Schedule
10.00
Presentation
10.15 – 11.15
Singularities in water waves and drops
Diego Córdoba (ICMAT)
11.15 – 11.45
Coffee break
11.45 – 12.45
Global Attractors
Anna Cima (UAB/BGSMath)

Diego Córdoba (ICMAT)
Biosketch
Diego Córdoba is a Professor at the Instituto de Ciencias Matemáticas (ICMat-CSIC) and the Scientific Director of the Severo Ochoa program 2016-2019. He obtained his PhD in Mathematics from Princeton University in 1998. He has held full time academic positions at the Institute for Advanced Study in Princeton (Member), University of Chicago (L. E. Dickson Instructor) and Princeton University (Assistant Professor ).
His research interest is focused on Partial Differential Equations, Analysis and Fluid Mechanics. He has coauthored over 60 research papers, including articles in Annals of Mathematics, Journal of the American Mathematical Society, Communications on Pure and Applied Mathematics, Duke Math. Journal, Communications in Mathematical Physics, Archives Rational Mechanics and Analysis, Journal of the European Mathematical Society and the Proceedings of the National Academy of Sciences USA.
Diego has been awarded an Alfred P. Sloan Doctoral Dissertation Fellowship (1997-1998), American Institute of Mathematics Postdoctoral Fellowship in 1999, Ramón y Cajal Researcher position in 2002, the SEMA Prize (Sociedad Española de Matemática Aplicada) for young researchers in 2005, and the Miguel Catalán Young Award 2011 from the Comunidad Autónoma de Madrid. In 2008 he obtained a Starting Independent Research Grant from the European Research Council (2008-2013). He was a Minerva Distinguished Visitor at the Math. Department of Princeton University from September 2014 until February 2015.
He has also been selected as an invited Speaker at the next International Congress of Mathematicians (ICM) in Rio de Janeiro, Brasil (2018).
Recently, Diego has been awarded an ERC Advanced Grant (2018-2023).

Anna Cima (UAB/BGSMath)
Biosketch
Professor at the Universitat Autònoma de Barcelona and member of the group GSD of Dynamical Systems at UAB, Anna Cima is a Catalan mathematician specialising in Dynamical Systems. Her fields on expertise includes Qualitative Theory of Planar Systems, Limit cycles, Global Attractors, Period Function, Abel Equation in the area of Continuous Dynamical Systems as well as Globally Periodic Maps, Dynamics of Rational Mappings, Integrable Systems, Linearisation of Periodic Maps in the area of Discrete Dynamical Systems.
She is the Master’s Coordinator of the Master’s Degree “Modelling for Science and Engineering” at UAB and a member of the BGSMath.
