PENTA NEWS
PENTA NEWS
Meet the algebraic topologist who helps biologists to analyse the brain
Kathryn Hess Bellwald was in Barcelona this spring for a Colloquium at the UAB, invited by BGSMath Faculty member & UAB Professor Natàlia Castellana. Topological vistas in neuroscience was an exciting excursion into how math tools can benefit biomedicine. In her case, the Blue Brain Project.
From top to bottom:
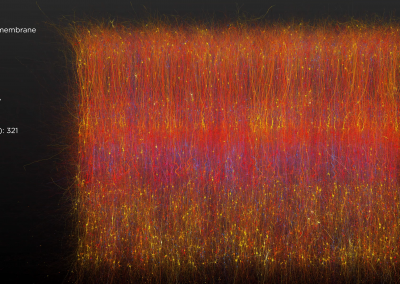
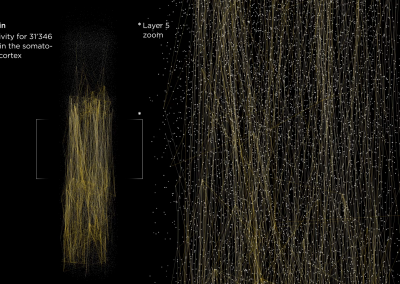
Three moments of Kathryn Hess’ Colloquim in Barcelona, at the Centre de Recerca Matemàtica (CRM); the last three images were presented by Prof. Hess during her presentation and are provided by the Blue Brain Project.
As many other brilliant mathematicians, US-born Kathryn Hess began her career very young. She graduated with a PhD from MIT when she was only 21. She then worked as a postdoc at the University of Stockholm, Nice, Toronto, and finally landed at the EPFL in 1999, where she holds the position of Associate Professor of Mathematics and Life Science since 2015. She is convinced that “biology needs all kinds of mathematics”. She says that, in her experience, “a lot of biologists have been very open to dialogue with mathematicians. They need help, their background in math is often not strong, but if mathematicians are willing to make an effort to understand their needs, they are very happy to collaborate”.
Tell us something about the Blue Brain Project.
The objective of the project is to reconstruct digitally and simulate activity in the brain of a rat, and ultimately the human brain. The human brain is formed by hundreds of billions of neurons and hundreds of trillions of synapses, through which electrical currents flow. The rat brain is smaller (2g vs 1.2 kg), but the structure is still complex, and its neocortex is similar. It has hundreds of millions of neurons and hundreds of billions of synapses! It’s like a “warm up” exercise for the human brain, but it’s still too much data to collect. So, we need to make a few well-chosen measurements to construct a model of the brain. The building blocks of the model are of course the neurons, the processing units of the brain. They come in different forms and shapes – there are 55 morphological types in our model! We use supercomputing to construct and simulate activity in this model, and we exploit the interconnections between biological experimental data. This way, we can produce models of the brain with very fine biological detail. The goal is to design a computer model of the rat’s neocortex as biologically accurate as possible in order to analyse its structure and functions.
What’s mathematics’ contribution to the project?
I entitled my talk “topological vistas” because I explore the many ways topology can be applied to neuroscience. For example, we examine neural activity through the filter of algebraic topology. It is normally difficult to see patterns in the firing of the neurons, but if we analyse the neural activity with the goggles of algebraic topology, we can see the mathematical signature of seemingly chaotic behaviour in the evolution of the firings with time. Algebraic topology describes the encoding process and perhaps will be able to visualize the moment the brain is making a decision. If we apply it to the “reconstructed neocortex”, the digital reconstruction of a 14-day old rat brain that was obtained in 2015, we can provide a description of its structure and function.
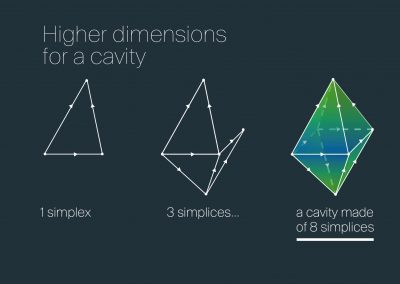
We make an abstract representation of circuits of neurons and how they connect together. We represent a neuron with a dot, and a connection with a segment. An arrow indicates a flow. We then construct “directed simplices” that represent families of neurons working together. The higher the “dimension” (a geometric representation of the structure in the neural network) of the simplices, the higher the coordination of the signal. We find that we have up to 8 neurons working together to amplify a signal. As you can see, algebraic topology has given us the tools to discern the inner structures in the brain and its functions.
Why is algebraic topology so useful for this kind of problems?
Applying graph theory to the analysis of the connectome (the map of neural connections in the brain) has already proved very useful in the past. This is not surprising for mathematicians, but perhaps it was a bit for neuroscientists. Algebraic topology is designed for the study of the notion of proximity and connectivity and of the emergence of global structure from local constraints. Furthermore, information usually flows in one direction in the brain, it cannot go backwards – the connections between neuron have a sense of direction imposed by the chemistry of the synapses. A perfect scenario to be tackled with algebraic topology.
Sometimes you say that “the brain is made up of ‘multi-dimensional geometrical structures”. This may sound a bit puzzling to the lay person. What do you mean?
People are often scared by the word “dimension”. It is just a way to say how big structures are. There are families of neurons working together to transmit messages further; the dimension is just the number of neurons working together (minus 1). If you represent these families geometrically, those are the dimensions that arise. The building blocks of the brain – i.e. the families of neurons – are put together in different ways. It’s like when you build a castle: how many windows and room does it have? In a topological space, we use something called Betti numbers: they count the cavities and loops arising from the way the neurons are connected together.
How can we be sure that algebraic topology is not an oversimplification of a biological complex phenomenon?
Because it reveals interesting information. One example is the functional role of simplices. The larger the group of neurons working together, the more highly correlated it is. Algebraic topology is able to quantify this. By using this mathematical filter, we can also manage to detect patterns in the way information flows through the brain that would be invisible otherwise.
How is the collaboration between mathematicians and biologists?
If there’s a good dialogue, it is easy to converge towards a model that works well. I have talked with a lot of biologists over the years, and it has always been easy to work together to set up good models. I, as a mathematician, have my own tool box, which does not always contain the right tools, though. The important message is that biology needs all kinds of mathematics. In my experience, a lot of biologists are looking for help. Their background in math is not always strong, but if mathematicians are willing to make an effort to understand their needs, they are very happy to work together with us.
What’s the next challenge you want to face?
Plasticity! We are studying what happens when some synapses become stronger, others weaker. One needs complex mathematical models for this – computation on grand scales. The Blue Brain Project is currently running plasticity simulations on a very powerful supercomputer at Argonne National Laboratory in the US, repeat patterns of stimuli, starting with a random distribution of strengths of synapses. After a while, neurons develop a preference for certain stimuli. We need more sophisticated topological tools for this analysis, since so far we have taken into account only whether there is a connection or not. In the future we intend to take into account the evolution of the weights of the synapses.
You attended a special program for talented children. Would you recommend it?
Not only would I recommend it full-heartedly, but I even created one at EPFL, called the Euler Course. It is open to any French-speaking child. We have an entrance exam, students taking it span from 9 to 13-years old. It’s a multiple-choice exam, and they are not familiar with most of the themes covered, so they have to work backwards from the possible answers. We also interview the children who do well on the exam together with their parents: we want truly motivated children, not those who are only pushed by their parents. We have approximately 25 students per class, and we simply replace their regular math course. Class is once per week for 3 hours in Lausanne and consists of lectures and exercises. The idea is that the first three years they just work through the regular school math programme, twice as fast, more in depth and more rigorously. After they finish school math, they begin university-level math. This way, those who want to do math at university can directly move to the second year; the others will just skip their math courses. It’s an incredible experience for them. Many are bored in school. With us, they learn how to think and how to structure their thought. Lots of them had never really studied before because it was too easy for them in school. They make good friends with people like them, hungry for knowledge just as they are. It replaces public schools, so we only charge a nominal fee of 100 francs per year, the rest is covered by EPFL and generous donors. For us it was extremely important that it was not just for children who could afford it.
You are a role model for many young female scientists. How is life for a woman in the mathematical world?
There were very few female role models when I was a child, few enough that I remember all of them. One was when I was in the accelerated programme myself. One day, a woman gave the only real math lecture about non-Euclidian geometry. It was exciting for me to discover that you could change the rules and the axioms and still get a functioning geometry! The most exciting thing I had ever heard was taught to me by a woman. Another one was at the university. At the time, I wanted to become an astrophysicist, so I took a lot of physics courses. One day, the teacher of my electromagnetism course, the only woman I ever had as a professor, told me: “you are doing very well in my course because you are a very good mathematician. But you have no physical intuition”. I was relieved – because being a physicist wasn’t coming naturally to me. She said something important to me at a crucial time of my life. Today, we are still too few women – and yes, I believe visibility is crucial for us!
Participants
Two videos describing Prof Hess’ research. The top one is from EPFL, the bottom one is a TED talk.