Sun Tzu approach to the Riemann Hypothesis
Sun Tzu approach to the Riemann Hypothesis
Summary
We give an introduction to the Riemann Hypothesis and a panoramic overview of the conjecture. We start with a historical introduction to transalgebraic ideas and continue with the classical theory of Riemann zeta function. We discuss some of the developments after Riemann that have contributed to a better understanding of the conjecture.
Audience
The target audience is general. The first session accessible to Master students.
Organiser: Eva Miranda (UPC – BGSMath)

Summary
We give an introduction to the Riemann Hypothesis and a panoramic overview of the conjecture. We start with a historical introduction to transalgebraic ideas and continue with the classical theory of Riemann zeta function. We discuss some of the developments after Riemann that have contributed to a better understanding of the conjecture.
Audience
The target audience is general. The first session accessible to Master students.
Organiser: Eva Miranda (UPC – BGSMath)
With the support of

AGAUR SGR
GEOMVAP 2017SGR932 “Geometria de Varietats i Aplicacions”

Vicente Muñoz Velázquez – University of Málaga
Biosketch
Vicente Muñoz received his PhD in 1996 at the University of Oxford (UK) under the supervision of Simon Donaldson. After this, he had positions Universidad Autónoma de Madrid, CSIC, and Universidad Complutense de Madrid, and he is currently Professor at Universidad de Málaga. He has had visiting fellowships at IAS Princeton (USA) in 2007 and Université Paris 13 (France) in 2015 and he has been a member of ICMAT (Spain), 2013-2016. His research interests lie in differential geometry, algebraic geometry and algebraic topology and, more specifically, gauge theory, moduli spaces, symplectic geometry, complex geometry and rational homotopy theory. He has published more than 100 research papers and the popular book “Las Formas que se Deforman” (editorial RBA), which has been translated into six languages.

Ricardo Pérez-Marco – CNRS & University of Paris Diderot
Biosketch
Programme (The Art of War)
Program (The Art of War)
DAY 1
Session 1.1: Transalgebraic theory. (The Weaponery) (Speaker: Ricardo Pérez)
1.1 Euler’s infinite series. Transalgebraic algebra.
1.2 Galois’ Galois theory. Transalgebraic number theory.
1.3 Riemann’s Riemann surfaces. Transalgebraic function theory.
Session 1.2: Riemann zeta function. (The Fortress) (Speaker: Ricardo Pérez)
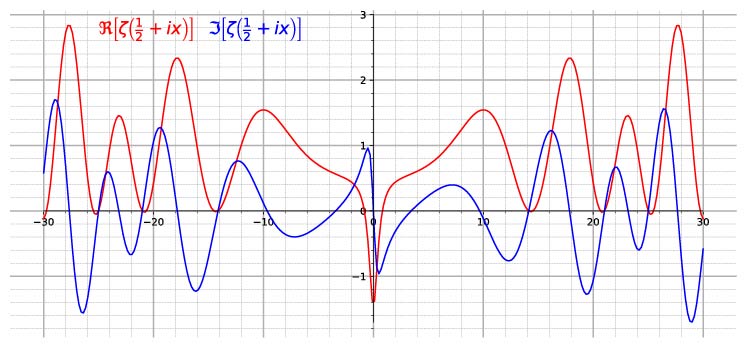
1.4 Basic theory of Riemann’s Zeta function.
1.5 Zeta function and prime numbers.
1.6 The Riemann Hypothesis.
1.7 Cramer function.
DAY 2
Session 2.1: First zoology of zeta functions. (The Enemy Territory) (Speaker: Ricardo Pérez)
2.1 Dedekind and Dirichlet L-functions.
2.2 Geometric zeta functions.
2.3 Dynamical and physical zeta functions.
2.4 Modular L-functions.
2.5 Kubota-Leopold zeta functions.
Session 2.2. Charting the territory around the RH (The Battlefield) (Speaker: Ricardo Pérez)
2.6 Euler product and the RH.
2.7 Functional equation and the RH.
2.8 Finite frequency RH.
2.9 Generalizations of the RH.
2.10 Classical attack propositions.
DAY 3
Session 3.1. Fourier analysis meets Number Theory (The Allies) (Speaker: Vicente Muñoz)
3.1 Poisson-Newton formula.
3.2 Application to zeta function and trace formulas.
Session 3.2. Gamma-functions (The Artillery) (Speaker: Vicente Muñoz)
3.3 Genus of meromorphic functions.
3.4 Hadamard regularization.
3.5 Gamma-functions and integral formulas.
DAY 4
Session 4.1. More insights (Tactic and Strategy) (Speaker: Ricardo Pérez)
4.1 Tate tools.
4.2 Polya approach.
4.3 Montgomery phenomenon.
4.3 Eñe product and the RH.
4.4 More statistics on Riemann zeros.
Session 4.2. Conclusions (The Battle Plan) (Speaker: Ricardo Pérez)
4.5 The necessary ingredients.
4.6 Scope of the conjecture.
4.7 Why it is difficult?
4.8 What it is important and what is not.
References
J.B. Conrey, The Riemann Hypothesis. Notices of the AMS, March, p.341-353, 2003.
H. M. Edwards, Riemann’s Zeta Function. Dover Publications, New York, 2001.
A. Ivic, The Riemann Zeta-Function. Theory and Applications. Dover Publications, New York, 1985.
V. Muñoz, R. Pérez-Marco, Unified treatment of Explicit and Trace Formulas via Poisson-Newton Formula. Comm. Math. Phys., 336, p.1201-1230, 2015.
B. Riemann, Über die Anzahl der Primzahlen unter einer gegebenen Grösse. Monatsberichte der Berliner Akademie, 1859.
Sun Tzu, The Art of War, 5th century BC.
